本文共 7073 字，大约阅读时间需要 23 分钟。

• 前言

1. 背景

2. 创意思路

• 功能及用法

• 相关技术

1. 粒子系统

2. 力

3. 音乐可视化

4. 分形

• 总结

---

《基于“分形”编写的交互应用》

前言

在上学期我们已经完成《互动媒体技术》课程的基础上，本学期进一步学习和应用了互动媒体的相关技术，与之前进行简单的有关”画笔”等基础操作不同，《代码本色》这本书介绍了大量与物理世界中各种现象、理论相对应的计算机实现，在此学习基础上制作了本次将要介绍的交互应用。

1. 背景

首先，在这门课程的整个学习中，给我留下最深刻的印象的有两个章节的内容，其中一个是“chp08_ fractals”（分形），第二个则是“ chp02_forces”（力)。究其原因，分形给我留下深刻印象是因为老师在课堂上所展示的几幅分形的画，这些画总结起来就是几个词——“无限、放大、自相似”，这种无限放大却始终能保持自相似的特性引起了我强烈的好奇心；而力这一章节给我留下深刻印象则是因为自己其实对于物理方面的知识很感兴趣，而正好这一章节将我对这方面的兴趣和我现在的专业结合了起来，将物理现象、理论通过以代码的方式将其展现了出来。

2. 创意思路

该应用使用了” chp02_forces”、 ” chp04_systems”、” chp08_fractals”这三章中的技术，实现了雪花飘落的景象并且通过交互操作实现雪球的形成与消失这两个过程。除此之外，结合了《游戏程序设计》这一课程中学习的音乐可视化的内容，将分形得到的图像与之相结合对所播放的背景音乐进行了音乐的可视化操作。

制作该交互应用想法的最初来源其实就是在学到”分形”这一章节时老师所展示的几幅画，被”分形”深深吸引之后，就想要来实现一个简单的分形，所以最终选择了koch曲线来实现雪花的绘制。 提到雪花，自然想到的是雪景，即大量的雪花，由此产生了制作雪花粒子系统的想法。这时候，有了单片的雪花、雪景（雪花粒子系统），那么雪堆积起来的所产生的另外一个有关雪花的形态——雪球就很容易联想到了。对于雪球，我该如何将其融入这个交互系统呢?此时就想到了“力”这个概念，牛顿所发现的万有引力定律指明了——任何物体之间都有相互吸引力，那么为何不可以将”万有引力”的物理效果进行一个放大呢，由此产生的想法是——雪球接近雪花->在雪球一定范围内的雪花被雪球吸附->雪球变大，质量变大->阻力增大，运动速度变慢。

---

功能及用法

由于该应用的交互操作比较简单，所以直接用视频的方式来展示该应用的功能及用法

---

技术

该系统用到了《代码本色》这本书中三个章节的内容，分别是” chp02_forces”、 ” chp04_systems”、 ” chp08_fractals”，由于该交互应用的最初想法来源于“分形”这一概念，并由此再联想展开到使用“力”和“粒子系统”并最终形成该交互应用，所以在本篇文章中将着重介绍“分形”这一技术并讲解在该系统中使用到的有关“分形”的地方。

1. 粒子系统

   1.1粒子系统技术的基本理论

   粒子系统是采用大量、具有一定声明和属性的微小粒子图元作为基本元素来绘制一个或多个对象。在粒子系统中，粒子图元的形状可以是小球、椭球、立方体或其他形状。每个粒子还具有大小、颜色、透明度、运动速度、运动方向和生命周期等属性。
   粒子在系统中要经过产生、运动和消亡三个阶段，期间粒子的大小、形状可能会随时间发生变化，其他性质如粒子的透明度、颜色和运动都随之改变，充分体现出不规则物体的动态性和随机性。
   粒子系统生成每一瞬间画面，一般都要进行一下基本步骤：
   ①：产生新的粒子加到系统中
   ②：为新生粒子设置初始属性
   ③：删除系统中已消亡的粒子
   ④：根据粒子的属性对粒子进行移动和变换：
   粒子的各种属性可以根据不同的经验函数确定，并给予一定的随机分布特性。

   1.2该应用中使用的粒子系统

   该应用中共使用到了两个粒子系统，一个是背景呈现雪景的粒子系统，该粒子系统中的单个粒子可以被雪球（鼠标控制）吸附；另一个粒子系统是点击鼠标产生的雪花喷射粒子系统，想要呈现出的效果是点击鼠标，雪球变小并开始喷射雪花直至雪球消失，该粒子系统中的单个粒子可与雪球之间产生万有引力的物理现象，但不会被雪球吸附。
   该应用中两个粒子系统有着相同的粒子图元，关于图元（分形雪花）的绘制在这儿就不作讲解了，对于分形雪花的制作的讲解将会放在后面的“分形”部分。

<1>雪景粒子系统：

粒子系统的基本实现步骤： ①：产生新的粒子加到系统中 ②：为新生粒子设置初始属性 ③：删除系统中已消亡的粒子

void update() {    Iterator
   
     ite = snowflakes.iterator();    while (ite.hasNext()) {      Snowflake s = ite.next();      s.update();      s.show();      if (s.position.y>(height+s.radius)) {        ite.remove();      }    }  }
   

④：根据粒子的属性对粒子进行移动和变换：

void update() {    position.add(velocity);    rotation +=aVelocity;  }

void show() {    pushMatrix();    //translate(position.x, position.y);    float x=position.x;    float y=position.y;    translate(x, y);    for (int i =0; i
   
     x-70-personlist.get(i).tm/2) && (personlist.get(i).ty > y-70-personlist.get(i).tm/2)) {       float targetXM = personlist.get(i).tx;        float kx = targetXM - position.x;        if(abs(kx) > 1) {          position.x += (kx * easing1)/10;       }              float targetYM = personlist.get(i).ty;        float ky = targetYM - position.y;        if(abs(ky) > 1) {          position.y += (ky * easing1)/10;       }               }     }    rotate(radians(rotation));    for (Branch b : branches) {      b.generate();    }    popMatrix();  }
   

<2>雪花喷射粒子系统：

粒子系统的基本实现步骤与雪景粒子系统类似，在这里就不再赘述，不同的是粒子系统中，所有粒子的初始位置都设置在了鼠标点击的位置（mouseX,mouseY） ，以及更新位置的方式。

espeedadd = new PVector(0,0.05);espeed = new PVector(random(-5, 5),random(-5, 0));

void update(){        espeed.add(espeedadd);        exy.add(espeed);        elife -= 10.0;    }

2. 力（万有引力）

由于在该应用中仅使用到了万有引力，且引力实现起来并不算复杂，所以在这儿就不做详细的描述了，在这儿仅展示一下最终的实现结果。

<1>雪花被雪球吸引导致改变运行轨迹:

<2>在雪球的一定范围内的雪花被雪球吸附，雪球变大，运动速度减慢:

3. 音乐可视化（不做详细介绍，仅展示结果）

4. 分形

无边的奇迹源自简单规则的无限重复。——benoit mondelbrot

分形通常被定义为"一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都(至少近似地)是整体缩小后的形状"，即具有自相似的性质。 自相似，即图形的每一部分与原图相似，无限放大均是与原图相似的。正是这种因无限次相同操作引起的自相似性，引发了一场不仅在数学界的革新，还在现代哲学的世界观和方法论上的革新。这种自相似性与老子的“人法地，地法天，天法道，道法自然”和莱布尼兹的“单子”相似 该交互应用的编写初衷是想要实现一个分形的实例，并且在该应用中，粒子系统的粒子元就是根据分形的知识来绘制的，可以说两个粒子系统就是在这个分形图形（粒子元）的基础上建立的，不仅如此，在完善该应用时做的音乐可视化也运用到了分形图形：更改分形图形的属性—大小来对音乐进行可视化操作。因此本篇文章将对“分形”进行详细的介绍以及对在应用中所用到的“分形”进行详细的分析。 首先来看看几张在课堂上引起我强烈兴趣的“分形图形” 这些“分形图形”都有一个共同特点——局部无限放大、自相似。而这些特征就涉及到了有关“分形”的另外一个概念——“分形几何学”。“天下万物生于有，有生于无，道生一，一生二，二生三，三生万物”，这句话很好地再现了“分形几何学”的特点。 分形几何学 分形几何学是一门以不规则几何形态为研究对象的几何学。相对于传统几何学的研究对象为整数维数，分形几何学的研究对象为非负实数维数。 一个数学意义上分形的生成是基于一个不断迭代的方程式，即一种基于递归的反馈系统。分形有几种类型，可以分别依据表现出的精确自相似性、半自相似性和统计自相似性来定义。 简单的说，分形就是研究无限复杂具备自相似结构的几何学。是大自然复杂表面下的内在数学秩序。 1.1 基本思想： 客观事物具有自相似的层次结构，局部与整体在形态、功能、信息、时间、空间等方面具有统计意义上的相似性，称为自相似性。例如，一块磁铁中的每一部分都像整体一样具有南北两极，不断分割下去，每一部分都具有和整体磁铁相同的磁场。这种自相似的层次结构，适当的放大或缩小几何尺寸，整个结构不变。 1.2 分形几何与传统几何相比的特点： ⑴从整体上看，分形几何图形是处处不规则的。例如，海岸线和山川形状，从远距离观察，其形状是极不规则的。 ⑵在不同尺度上，图形的规则性又是相同的。上述的海岸线和山川形状，从近距离观察，其局部形状又和整体形态相似，它们从整体到局部，都是自相似的。当然，也有一些分形几何图形，它们并不完全是自相似的。其中一些是用来描述一般随机现象的，还有一些是用来描述混沌和非线性系统的。

海岸线：

山脉分形图

瀑布分形 在该交互应用中，使用了两种不同的分形方式来绘制雪花，一种是类似于树的分形方式，另外一种则是使用Koch曲线进行的雪花绘制。 Koch曲线： Koch曲线性质： 1.它是一条连续的回线，永远不会自我相交。 2.它是一个无限构造的有限表达，每次变化面积都会增加，但是总面积是有限的，不会超过初始三角形的外接圆。 3.曲线是无限长的，即在有限空间里的无限长度。 4.它拥有自相似性，即将它放大之后会看到一个小的Koch雪花 Koch曲线构造方式： 对于一个等边三角形的每一条边三等分，将中间的一边换成等长的两边，再对每一条边进行相同的操作无限多次，即可得到Koch雪花。对于每一条边，包含4个Koch曲线，相似比为1:3，Koch雪花的豪斯道夫维度为log3 （4），介于一维和二维之间。每一条Koch曲线的每一条小边又是另一条Koch曲线。这是自相似性的体现。 在该系统使用的构造分形雪花的方式： <1>”树”形分形： 思路：构造一个”分形树”，将其作为雪花中的一瓣，然后再旋转连续旋转60°五次，最终形成分形雪花。 构造出的分形树： 实现：

void generate() {    pushMatrix();    rotate(radians(rotation));    float len=getStartLength(radius, ratio);    branch(len);    popMatrix();  }

void branch(float len) {    strokeWeight(len * 0.15);    strokeCap(ROUND);    line(0, 0, 0, -len);    translate(0, -len);        if (len > 1) {      pushMatrix();      branch(len * ratio);      popMatrix();      pushMatrix();      rotate(radians(-60));      branch(getStartLength(len, ratio));      popMatrix();      rotate(radians(60));      branch(getStartLength(len, ratio));    }  }

<2>Koch曲线：

思路: 给定线段AB，koch曲线可以由以下步骤生成： (1)将线段分成三等份（AC,CD,DB） (2)以CD为底，向外（内外随意）画一个等边三角形DMC (3)将线段CD移去 (4)分别对AC,CM,MD,DB重复1~3。 反复进行这一作图过程，得到的曲线越来越精细。 实现：

Segment[] generate(){    Segment[] children = new Segment[4];    PVector v = PVector.sub(b,a);    v.div(3);        //Segment 0    PVector b1 = PVector.add(a,v);    children[0] = new Segment(a,b1);    //Segment 3    PVector a1 = PVector.sub(b,v);    children[3] = new Segment(a1,b);        v.rotate(-PI/3);    PVector c = PVector.add(b1,v);    //Segment 1    children[1] = new Segment(b1,c);    //Segment 2    children[2] = new Segment(c,a1);    return children;  }

一般情况下，Koch雪花的构造会以图示中的A点作为原点,但在该系统中，由于想要用Koch雪花的大小来作为音乐可视化的一个度量，所以如果继续以A为原点进行绘制就会出现一些问题：

以A为原点：会导致整个雪花的放大缩小是以A点为放大缩小的中心点进行的。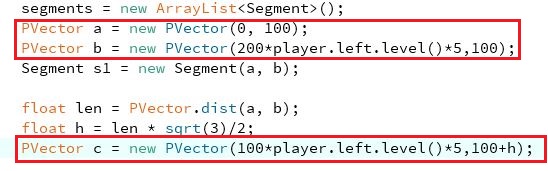

结果：

解决方式：将原点移动到雪花中心，重新计算相关点的坐标 结果：

---

总结

此次编写的这个交互应用的灵感来源于几张分形几何学的图片，并由此展开对于“分形”这一知识的学习，最终实现了最常见的分形图形——“koch雪花”。此外，结合粒子系统，将该分形图形作为粒子系统的粒子元，成功实现了两种粒子系统——雪景粒子系统、雪花喷射粒子系统。

对于“分形”这一知识的学习感触颇深，世界是非线性的，分形可以说是无处不在的，周海中教授认为：“分形几何不仅展示了数学之美，也揭示了世界的本质，还改变了人们理解自然奥秘的方式”。分形几何学不仅让人们感悟到科学与艺术的融合，数学与艺术审美的统一，而且还有其深刻的科学方法论意义。 分形的其中一个美丽之处即为有限与无限的结合。再接着说回koch曲线吧，每一次操作，一个koch曲线包含4个koch曲线，长度变为1／3，则每一次操作之后，长度增加4／3，进行无限次操作之后长度增加（4/3）^n，这是一个趋近正无穷的数，即无数次操作之后，长度变为正无穷。但是koch雪花的面积收敛到4/5 － 4/5 ＊ （4/9）^n，趋近于4/5，是一块有限的面积，这是有限的面积和无限的长度的结合。这种有限与无限的结合，有违常理，却又客观存在。曼德尔布罗特提出分形这一课题时的论文《英国的海岸线有无限长》 ，英国的面积有限，却拥有无限长的海岸线，现在测量海岸线也是一个难题。又如人体表面积的测量，人体表面介于二维和三维之间。英国海岸线的豪斯道夫维度为1.26，介于一维和二维之间。这种在低纬度无限，高维度有限的存在，连接了有限和无限。这又是分形引发的另一个革新。 有关“分形”可以让我们探索下去的还有很多很多，从最简单的艺术欣赏来说就足以让我们为之震撼。 下面给大家推荐几篇有关“分形之美”的欣赏的文章： 有关该交互应用的不足之处：功能其实过于单一，对于“分形”这一知识的使用还仅限于绘制简单的分形图形。对于“分形”的学习还远不足以让自己能用代码复现出上面连接中所展示的分形图像。该交互应用应该说是对于“分形”的一个小小的尝试吧，有关“分形”的知识还有很多很多有待去学习体会。

---

拓展： 一些分形作品展示

转载地址：http://quksi.baihongyu.com/